Enthalpy and Entropy of Vaporization of Water

    The purpose of this experiment is to determine the enthalpy and entropy of vaporization of water.

Entropy ( ΔS_vap ) is a concept we have not yet covered in class. For the purposes of this lab, read section 19.2 in your text. Think of it as just another value for vaporization, similar but different that enthalpy of vaporization, ΔH_vap.

Liquid vapor pressure comes about from molecules near the surface of the liquid having enough kinetic energy to liberate themselves from the iron grip of intermolecular forces in the liquid. As the temperature of the liquid increases, the vapor pressure also increases as more molecules have the minimum amount of energy to be liberated. The vapor pressure of a liquid at any temperature is also mathematically correlated with the enthalpy ΔH_vap and entropy ΔS_vap of  vaporization. The Clausius-Clapeyron equation describes this relationship:

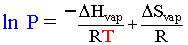
Everything in black is a constant in the above equation. Therefore if we make a graph of 1/T (x) vs. ln P (y) a straight line should exist with the slope correlated to ΔH_vap and the y-intercept correlated to ΔS_vap.  

The procedure will involve the measuring of a sample of gas (air + water vapor) at various temperatures. You will place an empty sealed flask into a container of cool water and connect a pressure sensor to it. The flask will be placed in a water bath on a hot plate set on low heat. A small sample (0.1-0.3 ml) of water is inserted into the flask. Water will begin to evaporate. As the temperature increases, the vapor pressure of water will increase. However, the pressure of the air that was already in the flask will also increase. This means that we will have to calculate the P_H2O at each step, as the pressure sensor measures total pressure at that temperature (P_total = P_air + P_H2Ovapor) 

The calculations in this experiment are ugly, and doing them by hand is a pain. I strongly urge you to use MS excel to do the data manipulation. The values you will need to calculate (in your spreadsheet) for each data point are:

- Absolute temperature
- Partial pressure of air sample (knowing n_air, T and V and using PV=nRT)
- Partial pressure of water vapor (P_total - P_air)
- Inverse absolute temperature (1/T) (for graph)
- ln P_H2O (for graph)

If you do it in columns, you can use these last two columns to get your straight line graph.

Lab report: I'm feeling nice, so you need to give me a summary, results and commentary sections only. One of the results you need to give is the temperature range of RAW DATA that gives the smallest % error between your values of  ΔH_vap and  ΔS_vap and the known values. This will require making and looking at several graphs. You will only include in your report ONE excel graph, that of the aforementioned best data subset. You neeed not give actual raw data nor sample calculations.

Prelab questions: (to be completed on a separate piece of recycled paper, handed to the instructor as you enter lab)

1. Ethanol has a ΔH_vap = 38.56 kJ/mol and ΔS_vap = 109.67 J/K mol. What is the vapor pressure of ethanol at 300. K? Show all your work. Watch your units! The units on the right hand side of the Clausius-Clapeyron equation all cancel out but is still equal to Ln P (which you would think needs a unit) That problem comes from the fact that you cannot take a logarithm of a unit. When you solve for the right hand side and take the anti-log, the units are atm. Thats is a product of the way the equation is derived.

~MEO 23Jan08