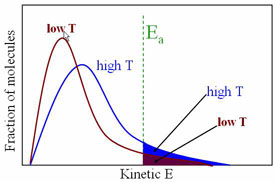
Effect of Temperature on rate of Reaction

The rate of reaction is a function of many things, including surface area, concentration and temperature. For a reaction to take place, the molecules must collide with enough energy (called the Activation Energy, E_A) Consider the reactant molecules to be at a particular temperature. By definition, the molecules have an average kinetic energy, some with more than the average, some with less. If we increase the temperature of a system, the average kinetic energy will increase and the number of molecules with the 'minimum' energy to react, thus increasing the frequency (rate) of reaction.

Svante Arrhenius has shown that for simple reactions, the equation

k = Ae^-Ea/RT   →   ln k = -E_A/RT + ln A

where k = rate constant, A is the collision frequency factor (function of the nature of reaction) R is the gas constant, T is the absolute temperature, E_A is the activation energy, and e is the base of the natural logarithms. We want to know the relationship between rate of reactions and two different temperatures. After some creative algebra, we can transform the Arrehenius equation into something manageable:

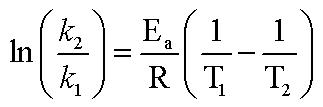
1 H₂O₂ + 2 HI → 2 H₂O + 1 I₂

This reaction has been shown to be a second order reaction, first with respect to [HI], first with respect to [H₂O₂]. The experimentally determined rate law is of the form:

rate = k[HI][H₂O₂]

The total volume of the solution containing the components of the reaction is kept constant during the course of this experiment. In fact, we keep everything constant for each run EXCEPT the temperature, so for our purposes, we can write the rate law as: rate = k (constant)

Since, in our equation we are looking at the ratios of the rate constants, and rate is directly proportional to rate constant (in our system here only because we are keeping everything constant) That means, instead of using the ratios of k's, we can use the ratios of rates instead.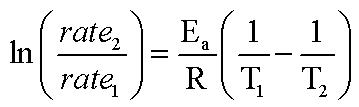

           

            Starch is added to this solution as the indicator of free iodine. We start the stopwatch at the moment we add our second reactant, H₂O₂. Of course the production of I₂ begins immediately, and the blue color will instantly appear. A measured volume of 0.1 M Na₂S₂O₃ is then added, causing the blue color to disappear due to the reduction of the I₂ by thiosulfate. The solution will stay colorless until enough additional I₂ is produced by H₂O₂-HI oxidation to react with the remaining Na₂S₂O₃ in the solution. At this point the blue color will reappear. The time is noted (stop stopwatch)  This represents the time required to produce I₂ equivalent to the Na₂S₂O₃ in the volume of 0.1 M Na₂S₂O₃ which was added. The entire reaction will be repeated with the same concentrations, but at a different temperature.

Wow, that is confusing. You probably wanna watch the explanation screencast a few times. 

Chemicals needed- 0.60 M KI (freshly made) , 0.100 M Na₂S₂O₃, 0.6% H₂O₂ (freshly made from 3% soln),  starch solution, 6M H₂SO₄, ice

 You will be running the entire reaction procedure (a minimum of) 4 times, once in a water-ice bath at around 0.0 °C, and 3x  at around 25 °C. The procedure below is the same for all runs.

 1. Add  your particular temperature of water (room T water or ice water) to a 1L beaker and a 400 mL beaker (let's call it the rxn beaker) with your particular temperature of water (room T water or ice water) The 1 L beaker with be a constant temperature bath for the rxn beaker, so it does not need that much.
2. Add 10.00 mL of KI using a volumetric pipet to the rxn beaker alone with ~200 mL of DI water. 
3. Add 15 mL of 6M H₂SO₄ (caution!) and carefully place the beaker in the 1L water (or ice for the low temp run) bath beaker. Place a stir bar in the solution and place the entire system on a stir plate and turn it on (no heat!!)
5. Add 5.00 mL of 0.6% H₂O₂ solution (using a volumetric pipet) and place it in a test tube, stopper it, and put it in the rxn beaker.
6. You want to wait until everything is at the desired temperature before you go any further. Once you start the reaction, you will want to keep the system stirring to keep everything at the same (water bath) temperature.
7. Add some starch indicator to the rxn beaker. Your instructor will tell you how much.
8. Add the H₂O₂ to the solution and begin timing. The solution should immediately turn blue. That’s a good thing. The stopwatch does not get stopped until that blue color returns (you are about to make it go away)
9.  WITHIN 30 SECONDS, Add 4.00 mL of 0.100 M Na₂S₂O₃ to the rxn beaker using a volumetric pipet.
10. Stop the stopwatch as soon as the solution STARTS to turn the blue/brown color again.

Three good runs at room T, calc rate, calc k for each run, average the three k's to get ONE k for that T.
One good run at near ice T (rxn temp needs to be lower than 4 C), calc rate, calc k 
Calc Ea from the two T's, and the two k's.

 For this experiment, you are writing a submitting a computer generated data sheet that has everything included for each run (measured T, time for rxn, rate of rxn, k for each run, average k for each set of T) The only sample calculation you need to show me is the Ea calc. Of course, you also need to add a short form memo style commentary section.
Prelab:

1. The decomposition of ethylene oxide at 652 K is the first-order reaction with k = 0.0120 min-1 and an activation energy of 218 kJ/mol. What is the RATE OF REACTION at 752 K?

                              (CH₂)₂O(g)  →  CH₄(g) + CO(g)
You will also need to show the instructor your premade computer generated data sheet before you step foot in the lab. No computer generated data sheet no lab for you!